تنش و کرنش موجود در تیرهای کامپوزیتی

تیرهای کامپوزیتی:
به تیرهایی که از دو یا چند ماده مختلف ساخته شده باشند، «تیرهای کامپوزیتی» (Composite Beams) گفته می شود.

محور_خنثی

تیرهای «دوفلزی» (Bimetallical) مورد استفاده در ترموستات ها، لوله های دارای پوشش پلاستیکی، تیرهای چوبی دارای صفحات تقویت کننده فولادی، نمونه هایی از تیرهای کامپوزیتی هستند که تصویر آن ها در شکل زیر نمایش داده شده است.

نمونه هایی از تیرهای کامپوزیتی:

الف) تیر دوفلزی؛
ب) لوله دارای پوشش پلاستیکی؛
ج) تیر چوبی دارای صفحات تقویت کننده فولادی.

در سال های اخیر، انواع متعددی از تیرهای کامپوزیتی وارد صنعت شده اند. هدف اصلی از به کارگیری این تیرها، صرفه جویی در مواد مصرفی و کاهش وزن سازه ها است.

«تیرهای ساندویچی» (Sandwich Beams) به عنوان یکی از انواع تیرهای کامپوزیتی، کاربرد وسیعی در صنایع هوایی و هوافضا دارند؛ چراکه در این صنایع، به کارگیری قطعات سبک با مقاومت و صلبیت بالا از اهمیت زیادی برخوردار است.

وسایل شناخته شده مختلفی نظیر قفسه های کتاب، جعبه های مقوایی، درها و … نیز به سبک تیرهای ساندویچی ساخته می شوند.

شکل زیر، نمونه هایی از تیرهای ساندویچی را نمایش می دهد. نمونه معمولی این تیر از دو صفحه نازک با مقاومت نسبتاً بالا (مانند صفحات آلومینیومی) و یک هسته ضخیم با وزن کم و مقاومت پایین (مانند پلاستیک) تشکیل می شود.

به دلیل فاصله زیاد صفحات از محور خنثی (محل رخ دادن بیشترین تنش خمشی)، رفتار آنها مشابه بال های یک تیر I شکل است. هسته تیر ساندویچی همانند یک پرکننده عمل می کند و نگهداری لازم برای صفحات را فراهم می سازد (این پیکربندی باعث جلوگیری از کمانش و چین خوردگی صفحات می شود).

پلاستیک و فوم های سبک اغلب برای هسته تیرهای کامپوزیتی مورد استفاده قرار می گیرند. در بخش بعدی، به معرفی نحوه تحلیل تیرهای کامپوزیتی می پردازیم.

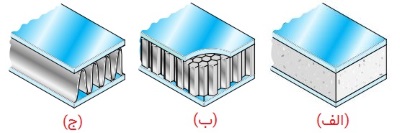
نمونه هایی از تیرهای ساندویچی:

الف) با هسته پلاستیکی؛
ب) با هسته کندویی؛
ج) با هسته موج دار

تنش و کرنش موجود در تیرهای کامپوزیتی:
با استفاده از اصول اولیه محاسبه کرنش های موجود در تیرهای متشکل از یک ماده می توان کرنش های موجود در تیرهای کامپوزیتی را نیز تعیین کرد (مخصوصاً اگر نقاط تشکیل دهنده مقاطع عرضی تیر در حین اعمال خمش بر روی صفحه قبلی خود باقی بمانند).

این قاعده همیشه برای حالت خمش خالص صدق می کند و به ماهیت ماده تشکیل دهنده تیر بستگی ندارد.

از این رو، در یک تیر کامپوزیتی میزان کرنش طولی εx با حرکت از سمت بالا تا پایین تیر به صورت خطی تغییر می کند. رابطه این کرنش عبارت است از:

y: فاصله نقطه مورد بررسی تا محور خنثی؛ ρ: شعاع انحنا؛ k: انحنا

برای محاسبه تنش و کرنش موجود در هر نوع تیر کامپوزیتی باید از رابطه بالا شروع کنیم. به منظور نمایش چگونگی اجرای این عملیات، تیر کامپوزیتی نمایش داده شده در شکل زیر را در نظر بگیرید. این تیر از دو ماده متفاوت (ماده 1 و 2) تشکیل شده است.

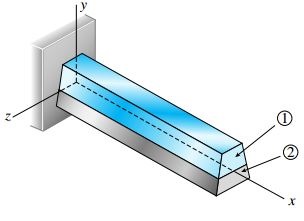
تیر کامپوزیتی متشکل از دو ماده

ترکیب دو ماده تشکیل دهنده تیر کامپوزیتی بالا به گونه ای است که می توان رفتار آن در برابر بارهای اعمال شده را مانند رفتار یک ماده واحد در نظر گرفت.

در شکل بالا، صفحه x-y را به عنوان صفحه تقارن و صفحه x-z را به عنوان صفحه خنثی تیر در نظر می گیریم. البته توجه، به دلیل استفاده از دو ماده برای ساخت این تیر، محور خنثی (محور z در شکل زیر) از مرکز هندسی عبور نمی کند.

سطح مقطع تیر کامپوزیتی متشکل از دو ماده

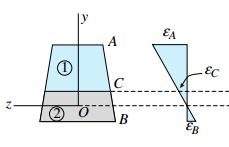
اگر تیر کامپوزیتی بالا با انحنای مثبت خم شود، کرنش های εx مانند شکل زیر تغییر می کنند. در این نمودار، کرنش فشاری موجود در بالای تیر با εA، کرنش کششی موجود در پایین تیر با εB و کرنش موجود در سطح اتصال دو ماده با εC نمایش داده شده است. به خاطر داشته باشید که هیچ کرنشی بر روی محور خنثی رخ نمی دهد.

توزیع کرنش‌های εx بر روی ارتفاع تیر

تنش های نرمال اعمال شده بر روی سطح مقطع با استفاده از کرنش های موجود و روابط تنش-کرنش مواد تشکیل دهنده تیر به دست می آیند.

با در نظر گرفتن رفتار الاستیک خطی برای مواد تشکیل دهنده تیر می توانیم از قانون هوک به منظور محاسبه تنش تک محوری کمک بگیریم. به این ترتیب، مقدار تنش های موجود در این مواد برابر حاصلضرب کرنش در مدول الاستیسیته خواهد بود.

در اینجا، مدول الاستیسیته ماده 1 و 2 را به ترتیب با حروف E1 و E2 نمایش می دهیم و فرض می کنیم که رابطه E2>E1 بین این دو مدول برقرار است. با در نظر گرفتن این نکات، یک نمودار توزیع تنش مطابق شکل زیر به دست می آید.

تنش فشاری اعمال شده بر بخش بالایی تیر با استفاده از رابطه σA=E1εA و تنش کششی موجود در بخش پایینی آن با استفاده از رابطه σB=E2εB محاسبه می شود.

توزیع تنش‌های σx برای حالت E2>E1

در سطح اتصال C، تنش های موجود در هر ماده با یکدیگر تفاوت دارند. دلیل این اختلاف، برابر نبودن مدول الاستیسیته مواد است. مقدار این تنش ها در ماده 1، از رابطه σ1C=E1εC و در ماده 2، از رابطه σ2C=E2εC به دست می آید.

با کمک قانون هوک و رابطه کرنش طولی εx می توانیم تنش های نرمال موجود در فاصله y از محور خنثی را بر اساس مفهوم انحنا بیان کنیم: