رابطه گشتاور-انحنا و تنش های نرمال در تیر کامپوزیتی

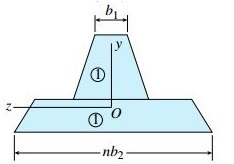
رابطه گشتاور-انحنا و تنش های نرمال در تیر کامپوزیتی:

رابطه گشتاور-انحنا برای تیر معادل باید با رابطه مربوط به تیر اصلی برابر باشد. به منظور تأیید صحت این مسئله، به خاطر داشته باشید که تنش های موجود در تیر معادل (متشکل از ماده 1) از طریق رابطه زیر محاسبه می شود:

با استفاده از رابطه بالا و همچنین روند تشریح شده در مبحث «تنش های نرمال موجود در تیرها»، رابطه گشتاور-انحنا برای تیر معادل به دست می آید:

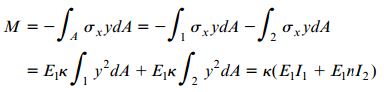
یا

معادله بالا مشابه با معادله معرفی شده در مبحث «مبانی تحلیل تیرهای کامپوزیتی» است. به این ترتیب، صحت فرض برابر بودن رابطه گشتاور-انحنا تیر معادل با تیر اصلی تأیید می شود.

تنش های نرمال:
به دلیل واحد بودن ماده تشکیل دهنده تیر معادل، می توان مقدار تنش های نرمال و همچنین تنش های خمشی موجود در آن را با استفاده از رابطه پیچش محاسبه کرد.

بنابراین، تنش های اعمال شده به این تیر از رابطه زیر به دست می آید:

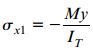
IT: ممان اینرسی مقطع معادل نسبت به محور خنثی

با جایگذاری مختصات محور خنثی، مقدار گشتاور خمشی و ممان اینرسی در رابطه بالا می توانید میزان تنش های اعمال شده بر هر نقطه دلخواه در تیر معادل را محاسبه کنید.

اگر رابطه بین ممان اینرسی مقطع معادل و ممان اینرسی مقطع اولیه را به صورت زیر در نظر بگیریم:

سپس، عبارت های رابطه IT را درون رابطه بالا قرار دهیم، خواهیم داشت:

این رابطه با رابطه اول پیچش برای تیرهای کامپوزیتی برابر است. در نتیجه، مقدار تنش های موجود در ماده 1 (تیر اصلی) با تنش های موجود در بخش متناظر آن در تیر معادل تفاوتی نخواهد داشت. این نکته، صحت رابطه تنش های نرمال موجود در تیر معادل را تأیید می کند.

توجه داشته باشید که تنش های موجود در ماده 2 (تیر اصلی) با تنش های موجود در بخش متناظر آن در تیر معادل برابر نیستند.

برای انجام محاسبات در این بخش باید تنش های تیر معادل را در نسبت مدولی n ضرب کنیم تا تنش های تیر اصلی به دست آید:

به منظور تأیید صحت رابطه بالا، عبارت های موجود در رابطه IT را درون آن قرار می دهیم:

این رابطه با رابطه دوم پیچش برای تیرهای کامپوزیتی برابر است.

نکات تکمیلی:
در مطالب ارائه شده راجع به نحوه به کارگیری روش مقطع معادل، تیر اصلی را به یک تیر متشکل از ماده 1 تبدیل کردیم.

توجه داشته باشید که امکان تبدیل تیر اصلی به یک تیر متشکل از ماده 2 نیز وجود دارد. در این حالت، تنش های موجود در ماده 2 تیر اصلی با تنش های موجود در بخش متناظر آن در تیر معادل برابر خواهد بود.

اگرچه، برای تعیین تنش های موجود در ماده 1 تیر اصلی باید تنش های بخش متناظر را در نسبت مدولی n ضرب کنیم. رابطه نسبت مدولی در این حالت برابر n=E1/E2 است.

علاوه بر نکته بالا، امکان تبدیل تیر اصلی به یک تیر متشکل از ماده ای با هر مدول الاستیسیته دلخواه نیز وجود دارد.

در این حالت، ابعاد تمام بخش های تیر به ابعاد تیر جدید تبدیل می شوند. اگرچه، با تبدیل مواد به یکی از مواد موجود در تیر، محاسبات مورد نیاز ساده تر خواهند بود.

با کمی خلاقیت و ابتکار می توان از روش مقطع معادل برای تحلیل تیرهای کامپوزیتی متشکل مواد بیشتر نیز استفاده کرد.