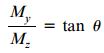تحلیل تیرهای دارای تقارن مضاعف تحت بارگذاری مورب:
برای شروع تحلیل تیرهای دارای تقارن مضاعف، شکل زیر را در نظر بگیرید. در این تیر، هر دو صفحه xy و xz به عنوان صفحات تقارن به حساب می آیند.
به منظور جلوگیری از ایجاد پیچش در حول محور طولی تیر، فرض می کنیم که محل اعمال بار مورب از مرکز هندسی سطح مقطع عبور می کند.
مقدار تنش های خمشی موجود در تیر بالا از تجزیه بار مورب به دو مؤلفه اعمال شده بر صفحات تقارن به دست می آید.
پس از تعیین تنش های خمشی مربوط به هر یک از مؤلفه ها با استفاده از رابطه پیچش، مقدار تنش نهایی از برهم نهی این تنش ها محاسبه می شود.
قواعد علامت گذاری گشتاورهای خمشی:
یکی از نکات اصلی در تحلیل گشتاورهای خمشی، تعیین قواعد علامت گذاری پیش از شروع تحلیل است.
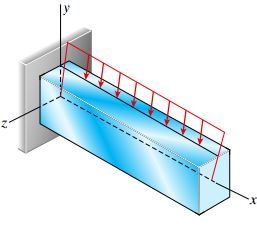
به این منظور، با ایجاد یک برش درون تیر، وضعیت بارهای اعمال شده بر سطح مقطع آن را مطابق شکل زیر مورد بررسی قرار می دهیم.
در شکل زیر از بردارهای دو پیکانی برای نمایش گشتاور خمشی My حول محور y و گشتاور خمشی Mz حول محور z استفاده شده است.
اگر نوک پیکان بردار گشتاور به سمت مثبت محور مربوطه اشاره کند، علامت آن مثبت خواهد بود.
جهت چرخش گشتاور با استفاده از قانون دست راست بردارها به دست می آید (با قرار دادن انگشت شست در راستای اعمال بردار و تعیین ساعت گرد/پادساعت گرد بودن جهت چرخش با بررسی جهت چرخش باقی انگشت ها).
با توجه به شکل بالا، گشتاور خمشی مثبت My باعث ایجاد فشار در بخش سمت راست تیر (بخش منفی محور z) و کشش در بخش سمت چپ آن (بخش مثبت محور z) می شود.
به همین ترتیب، گشتاور خمشی مثبت Mz، بخش بالایی تیر (بخش مثبت محور y) را تحت فشار و بخش پایینی آن (بخش منفی محور y) را تحت کشش قرار می دهد.
علاوه بر این، توجه داشته باشید که گشتاورهای خمشی نمایش داده شده در شکل بالا، بر روی بخش مثبت محور x اعمال می شوند.
در نتیجه، این گشتاورها بر وی صفحه ای قرار دارند که بردار نرمالش به جهت مثبت محور x اشاره می کند.
تنش های نرمال (تنش های خمشی):
تنش های نرمال حاصل از اعمال گشتاورهای خمشی My و Mz توسط رابطه پیچش مورد ارزیابی قرار می گیرند.
پس از تعیین این تنش ها، تنش های ناشی از اعمال هم زمان گشتاورها با استفاده از برهم نهی تنش های نرمال محاسبه می شوند. به عنوان مثال، تنش های موجود در یکی از نقاط موجود بر روی مقطع عرضی زیر (نقطه A) را در نظر بگیرید. این نقطه در بخش مثبت محورهای y و z قرار دارد.
اعمال گشتاور مثبت My باعث ایجاد کشش در نقطه A و اعمال گشتاور مثبت Mz منجر به ایجاد کشش در نقطه مذکور می شود. به این ترتیب، تنش نرمال در نقطه A برابر است با:
Iy و Iz به ترتیب ممان اینرسی سطح مقطع تیر نسبت به محورهای y و z را نمایش می دهند. با استفاده از رابطه بالا می توان تنش های نرمال موجود در هر نقطه دلخواه بر روی سطح مقطع را محاسبه کرد. به این منظور، تنها باید مقادیر جبری گشتاورها و مختصات آن ها را درون این رابطه قرار داد.
محور خنثی:
اگر تنش نرمال σx را برابر با صفر قرار دهیم، معادله مورد نیاز برای تعیین مختصات محور خنثی به دست می آید:
این معادله نشان می دهد که محور خنثی nn به صورت یک خط راست گذرنده از مرکز هندسی C است.
زاویه بین محور خنثی و محور z از طریق رابطه زیر محاسبه می شود:
زاویه β بین مقادیر °90- تا °90+ تغییر می کند. مقدار و علامت به دست آمده برای این زاویه به مقدار و جهت گیری گشتاورهای خمشی بستگی دارد.
اطلاع از نحوه جهت گیری محور خنثی برای تعیین محل رخ دادن تنش نرمال ماکسیمم بر روی مقطع عرضی به کار می آید. به دلیل رابطه خطی بین مقدار تنش و فاصله آن ها تا محور خنثی، تنش ماکسیمم در دورترین نقطه (بیشترین فاصله) از محور خنثی رخ می دهد.
رابطه بین محور خنثی و زاویه اعمال بار:
همان طور که در بخش قبلی نیز اشاره شد، جهت گیری محور خنثی نسبت به محور z با استفاده از گشتاورهای خمشی و ممان های اینرسی مشخص می شود. مرحله بعدی، تعیین جهت گیری محور خنثی نسبت به زاویه اعمال بار بر روی تیر است.
به این منظور، تیر یکسر گیردار زیر را در نظر بگیرید. این تیر در معرض نیروی P قرار دارد که بر روی آخرین مقطع عرضی تیر اعمال می شود. زاویه بین نیروی مذکور با جهت مثبت محور y برابر با θ است. در این جهت گیری به خصوص، گشتاورهای خمشی My و Mz در محدوده θ=0 تا °θ=90 دارای علامت مثبت هستند.
به منظور تسهیل فرآیند تحلیل می توانیم بار P را به دو مؤلفه Pcosθ در جهت مثبت محور y و Psinθ در جهت منفی محور z تجزیه کنیم. به این ترتیب، گشتاورهای خمشی اعمال شده بر سطح مقطع (My و Mz) در فاصله x از تکیه گاه ثابت تیر از روابط زیر به دست می آیند:
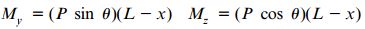
L: طول تیر
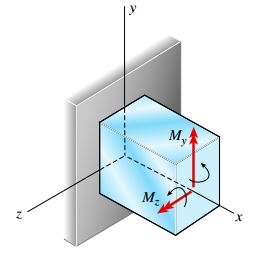
نسبت این دو گشتاور برابر است با:
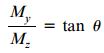
نسبت بالا نشان می دهد که بردار برآیند گشتاور M در زاویه θ نسبت به محور z قرار دارد. در نتیجه، بردار برآیند گشتاور به صفحه طولی دربرگیرنده نیروی P عمود است. مقدار زاویه β در فاصله بین محور خنثی nn و محور z نیز به صورت زیر تعیین می شود:
طبق رابطه بالا، زاویه β معمولاً با زاویه θ برابر نیست. بنابراین، محور خنثی در اغلب موارد بر صفحه طولی دربرگیرنده بار اعمال شده عمود نخواهد بود؛ مگر اینکه یکی از حالت های خاص زیر در مسئله وجود داشته باشد:
در حالت سوم از موارد بالا، تمام محورهای گذرنده از مرکز هندسی سطح مقطع به عنوان محورهای اصلی در نظر گرفته می شوند؛ چراکه مقدار ممان اینرسی تمامی آن ها با یکدیگر برابر است.
صفحه اعمال بار نیز همیشه به عنوان یکی از صفحات اصلی بوده و بر محور خنثی عمود است. این حالت در تیرهایی با سطح مقطع دایره ای و مربعی رخ می دهد.
به این ترتیب در حالت کلی، هیچ الزامی به عمود بودن محور خنثی بر صفحه اعمال بار وجود ندارد. این نکته، تأثیر زیادی بر روی تنش های موجود در تیر می گذارد؛ مخصوصاً اگر نسبت ممان های اینرسی اصلی عدد بزرگی باشد.
در این شرایط، حساسیت تنش های موجود در تیر به تغییر جهت اعمال بار و همچنین تغییر راستای تیر افزایش می یابد. در مثال های انتهای مقاله می توان این ویژگی را به خوبی مشاهده کرد.
|
|
|
|
| نماد اعتماد الکترونیک | نشان ملی ثبت | گواهی شامد ارشاد |
© کلیه حقوق مادی و معنوی این وب سایت متعلق به داده پردازان هومان پویان می باشد.
