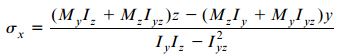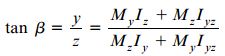روشی دیگر برای تحلیل تیرهای نامتقارن

روشی دیگر برای تحلیل تیرهای نامتقارن:
در بخش های قبلی، به معرفی تحلیل تیر نامتقارن با استفاده از تعیین موقعیت محورهای اصلی مرکزی سطح مقطع و تجزیه گشتاور خمشی به مؤلفه های هم جهت با این محورها پرداختیم.

مزیت اصلی روش مذکور، امکان به کارگیری تمام روابط موجود برای محاسبه تنش ها و تغییر شکل های اعمال شده بر تیر است.

با این وجود، اگر جهت گیری محورهای اصلی با استفاده از جداول یا بررسی سطح مقطع امکان پذیر نباشد، دشواری روش افزایش می یابد.

در صورت نیاز به محاسبه جهت گیری محورهای اصلی و مقدار ممان های اینرسی اصلی، کار با «محورهای غیر اصلی مرکزی» (Nonprincipal Centroidal Axes) که هم راستا با اضلاع سطح مقطع هستند، روند تحلیل را ساده تر می کند (مانند شکل زیر).

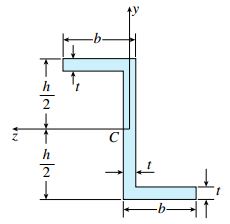
به منظور تعمیم معادلات خمش برای محورهای غیر اصلی، سطح مقطع نامتقارن نمایش داده شده در شکل زیر را در نظر بگیرید.

با وجود اینکه مبدأ محورهای y و z بر روی مرکز هندسی سطح مقطع قرار دارد، این محورها به عنوان محورهای اصلی به حساب نمی آیند.

گشتاورهای خمشی My و Mz بر روی سطح مقطع اعمال می شوند و خمش بر روی صفحات xy و xz رخ می دهد. با این وجود، صفحات مذکور جز صفحات اصلی نیستند.

اگر انحنای صفحات xy و xz به ترتیب برابر ky و kz باشد، تنش نرمال اعمال شده بر نقطه A برابر است با:

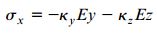
اگر برآیند نیروی محوری اعمال شده بر سطح مقطع در راستای x را برابر صفر قرار دهیم، خواهیم داشت:

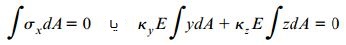
این معادله بدون هیچ تغییری قابل استفاده است؛ چراکه مبدأ محورهای فرضی از مرکز هندسی سطح مقطع تیر عبور می کند. به این ترتیب، گشتاور My برابر با برآیند گشتاور حول محور y است:

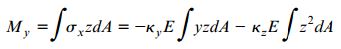
به عبارت دیگر:

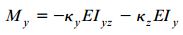
Iyz: حاصل ضرب اینرسی سطح مقطع نسبت به محورهای y و z

به همین ترتیب، رابطه گشتاور حول محور z برابر است با:

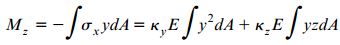
به عبارت دیگر:

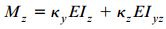
در صورت حل همزمان معادلات گشتاور حول محور y و z، رابطه تعیین انحنا بر حسب گشتاورهای خمشی به دست می آید:

اگر مقادیر My و Mz مشخص باشند، با جایگذاری عبارت های بالا در رابطه σx=-kyEy-kzEz می توان مقدار تنش نرمال σx در هر نقطه دلخواه بر روی یک تیر نامتقارن را تعیین کرد:

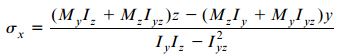
معادله بالا، «رابطه تعمیم یافته پیچش» (Generalized Flexure Formula) برای تیرهای نامتقارن را نمایش می دهد.

در این رابطه، مؤلفه های گشتاور حول محورهای مرکزی متعامد اعمال می شوند و هیچ ضرورتی در اصلی بودن این محورها وجود ندارد.

توجه داشته باشید که اگر محورهای y و z، محورهای اصلی مرکزی باشند، رابطه بالا به رابطه σx در روش قبلی تبدیل می شود؛ چراکه در این حالت، Iyz برای محورهای اصلی برابر با صفر خواهد بود.

اگر رابطه σx را برابر با صفر قرار دهیم، زاویه β بین محور z و محور خنثی و در نتیجه، جهت گیری محور خنثی nn به دست می آید:

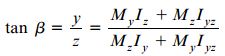
به این ترتیب، صفحه رخ دادن خمش بر محور خنثی عمود است.