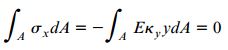مبانی تحلیل تیرهای نامتقارن:
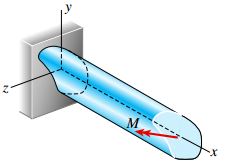
برای آشنایی با کلیت شرایط موجود در تحلیل خمش تیرهای نامتقارن، شکل زیر را در نظر بگیرید.
این شکل، یک تیر نامتقارن را نمایش می دهد که سطح مقطع انتهایی آن در معرض گشتاور خمشی M قرار گرفته است. در اینجا می خواهیم مقدار تنش های موجود در این تیر و محل قرارگیری محور خنثی آن را مورد ارزیابی قرار دهیم.
متأسفانه در این سطح از تحلیل، هیچ روش مستقیمی برای تعیین پارامترهای مذکور وجود ندارد. از این رو، به جای تعیین گشتاور خمشی و سپس محور خنثی، ابتدا یک محور خنثی فرضی را در نظر می گیریم و سپس میزان گشتاور خمشی را نسبت به آن می سنجیم.
محور خنثی:
به منظور شروع تحلیل، دو محور عمود بر هم (مانند محورهای y و z در شکل زیر) را در یک نقطه دلخواه بر روی سطح مقطع تیر در نظر می گیریم. محورهای فرضی می توانند در هر جهت دلخواهی قرار داشته باشند. با این وجود، به منظور تسهیل فرآیند تحلیل، جهت گیری عمودی و افقی را برایشان انتخاب می کنیم.
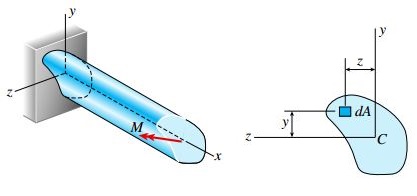
در مرحله بعد، فرض می کنیم که تیر به گونه ای خم می شود که محور خنثی مقطع عرضی آن همان محور z باشد. بر اساس این فرض، تغییر شکل تیر در صفحه xy (صفحه خمش) رخ می دهد.
تحت این شرایط، رابطه مورد نیاز برای محاسبه تنش نرمال اعمال شده بر المان سطح dA (در فاصله y از محور خنثی) به صورت زیر خواهد بود:
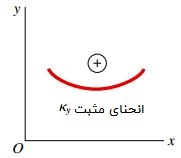
در صورت مثبت بودن انحنا، علامت منفی در پشت رابطه بالا به معنای فشاری بودن تنش اعمال شده بر بخش بالای محور z است. شکل زیر، قواعد علامت گذاری انحنا با فرض رخ دادن خمش در صفحه xy را نمایش می دهد.
نیروی اعمال شده بر المان سطح dA برابر σxdA است. به این ترتیب، برآیند نیروی اعمال شده بر تمام سطح مقطع تیر از انتگرال المان نیرو در محدوده سطح مقطع A به دست می آید. از آنجایی که تیر در معرض خمش خالص قرار دارد، برآیند نیرو در محدوده A برابر با صفر می شود:
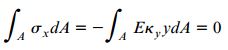
مدول الاستیسیته و انحنا در تمام سطح مقطع ها دارای یک مقدار ثابت هستند. از این رو:
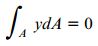
معادله بالا نشان می دهد که محور z (محور خنثی) از مرکز هندسی سطح مقطع (نقطه C) می گذرد.
اکنون فرض کنید که محور خنثی سطح مقطع در هنگام خمش تیر، محور y و صفحه خمش آن، صفحه xz باشد.
بر اساس این فرض، رابطه مورد نیاز براتی تعیین تنش نرمال اعمال شده بر المان سطح dA برابر است با:
شکل زیر، قواعد علامت گذاری انحنا با فرض رخ دادن خمش در صفحه xy را نمایش می دهد. در صورت مثبت بودن انحنا در صفحه xz، المان dA تحت فشار قرار خواهد داشت. در این حالت باید از یک علامت منفی پشت رابطه بالا استفاده کرد.
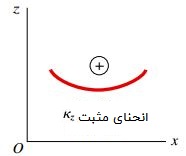
برآیند نیرو برای این حالت از رابطه زیر به دست می آید:
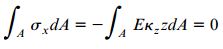
به این ترتیب داریم:
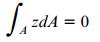
توجه داشته باشید که در رابطه بالا نیز محور خنثی از مرکز هندسی سطح مقطع عبور می کند.
بنابراین می توان نتیجه گرفت که مبدأ محورهای y و z برای یک تیر نامتقارن باید در مرکز هندسی آن قرار داشته باشد.
اکنون برآیند گشتاورهای تنش σx را در نظر بگیرید و دوباره فرض کنید که خمش تیر نسبت به محور z رخ می دهد.
به این ترتیب، گشتاورهای Mz و My حول محورهای z و y برابرند با:
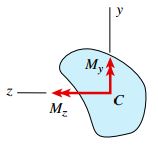
Iz: ممان اینرسی سطح مقطع عرضی تیر نسبت به محور z و Iyz: «حاصل ضرب اینرسی» (Product of Inertia) نسبت به محورهای y و z
با توجه روابط بالا می توان به نتایج زیر دست یافت:
اکنون محور y را به عنوان محور خنثی در نظر می گیریم و محاسبات قبلی را بر اساس این فرض تکرار می کنیم:
Iy: ممان اینرسی نسبت به محور y
در این حالت نیز مشاهده می کنیم که با انتخاب یک جهت گیری دلخواه برای محور y (محور خنثی)، گشتاورهای My و Mz بر روی تیر اعمال می شوند.
با این وجود، در صورتی که محور y به عنوان محور اصلی در نظر گرفته شود، My تنها گشتاور موجود در تیر و صفحه xz، محل رخ دادن خمش خواهد بود. در این شرایط نیز تیر نامتقارن همانند تیر متقارن رفتار می کند.
به دلیل عمود بودن محورهای y و z، اگر هر یک از آن ها به عنوان محور اصلی در نظر گرفته شود، محور دیگر نیز اصلی خواهد بود.
مهم ترین نتیجه ای که می توان از مباحث بالا گرفت، به صورت خلاصه در پاراگراف زیر آورده شده است:
در صورت اعمال خمش خالص بر روی یک تیر نامتقارن، صفحه دربرگیرنده گشتاور خمشی عمود بر صفحه خنثی خواهد بود؛ اگر محورهای y و z، محورهای اصلی گذرنده از مرکز هندسی (محورهای اصلی مرکزی) سطح مقطع تیر بوده و گشتاور خمشی اعمال شده، بر روی یکی از صفحات اصلی (صفحه xy یا xz) قرار داشته باشد.
با کمک این نتیجه می توان یک روش مستقیم را برای یافتن تنش های موجود در تیرهای نامتقارن (تحت یک گشتاور خمشی اعمال شده در یک راستای دلخواه) توسعه داد.
|
|
|
|
| نماد اعتماد الکترونیک | نشان ملی ثبت | گواهی شامد ارشاد |
© کلیه حقوق مادی و معنوی این وب سایت متعلق به داده پردازان هومان پویان می باشد.
