مقاطع متشکل از دو چهارضلعی متقاطع

مقاطع متشکل از دو چهارضلعی متقاطع:
در بخش قبلی، نیروها و تنش های برشی موجود در اضلاع نبشی را مورد بررسی قرار دادیم. هدف این تحلیل، معرفی یک روش کلی برای تحلیل مقاطع جدار نازک باز بود.

با این وجود، در صورتی که یافتن محل قرارگیری مرکز برش تنها هدف مسئله باشد، تعیین نیروها و تنش های برشی لزومی نخواهد داشت.

از آنجایی که تنش های برشی با محور مرکزی اضلاع موازی هستند، دو نیروی F به عنوان برآیندهای تنش های موجود در هر ضلع در نظر گرفته می شود.

برآیند این دو نیرو، یک نیروی گذرنده از محل تقاطع آن ها است.

در نتیجه، مرکز برش در این محل قرار دارد. به این ترتیب، می توان با یک استدلال تصویری ساده و بدون استفاده از هر گونه محاسباتی، محل قرارگیری مرکز برش یک مقطع نبشی با اضلاع برابر را تعیین کرد.

مطالب بالا برای مقاطع متشکل از دو چهارضلعی نازک متقاطع نیز قابل تعمیم است (شکل زیر).

در این موارد، برآیند تنش های برشی، نیروهایی هستند که در محل تقاطع چهارضلعی ها به هم برخورد کرده اند. بنابراین، مرکز برش آن ها در محل مذکور قرار خواهد داشت.

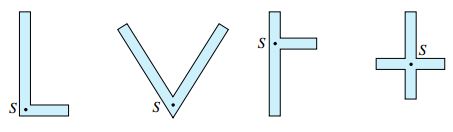
مرکز برش مقاطع متشکل از دو چهارضلعی نازک

مقطع Z:
در این بخش، به بررسی محل قرارگیری مرکز برش یک مقطع Z با جدارهای نازک می پردازیم (شکل زیر). این نوع مقطع هیچ محور تقارنی ندارد اما حول مرکز هندسی سطح خود دارای تقارن است.

محورهای y و z نیز محورهای اصلی گذرنده از مرکز هندسی سطح مقطع هستند.

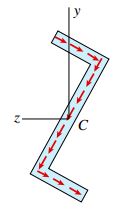
مرکز برش مقطع Z جدار نازک

در مرحله اول تحلیل، فرض می کنیم که یک نیروی برشی Vy به صورت موازی با محور y بر سطح مقطع اعمال شده و باعث ایجاد خمش حول محور z (محور خنثی) می شود. در این شرایط، جهت گیری تنش های برشی موجود در جان و بال های تیر مطابق شکل بالا است.

با توجه به وجود تقارن در سطح مقطع، نیروهای F1 موجود در بال ها با هم برابر خواهند بود (شکل زیر). برآیند سه نیروی موجود در سطح مقطع (دو نیروی F1 در بال ها و نیروی F2 در جان) باید با نیروی برشی Vy برابر باشد.

یروهای F1 دارای برآیند 2F1 هستند. این برآیند از مرکز هندسی سطح مقطع عبور می کند و جهت گیری آن با راستای بال ها موازی است. برآیند 2F1 نیروی F2 را در مرکز هندسی C قطع می کند. به همین دلیل، خط اثر نیروی برشی Vy باید از مرکز هندسی سطح مقطع بگذرد.

اگر تیر مورد نظر تحت نیروی برشی Vy قرار گیرد و این نیرو موازی با محور z باشد، Vy از مرکز هندسی سطح مقطع عبور خواهد کرد.

به دلیل قرارگیری مرکز برش در محل تقاطع دو نیروی برشی، مرکز برش مقطع Z با مرکز هندسی سطح آن تلاقی دارد.

این نتیجه گیری برای تمام مقاطع Z دارای تقارن نقطه ای حول مرکز هندسی صادق است (تمام مقاطع Z که بال های آن ها دارای عرض و ضخامت یکسان باشند).

با این وجود، هیچ الزامی برای برابر بودن ضخامت جان با ضخامت بال های تیر وجود ندارد. در ادامه، یک مثال متفاوت از مقاطع جدار نازک باز را مورد تحلیل و بررسی قرار می دهیم.

مثال:
شکل زیر، یک مقطع جدا نازک نیم دایره ای با شعاع r و ضخامت t را نمایش می دهد. فاصله e از مرکز نیم دایره در نقطه O تا مرکز برش S را تعیین کنید.

مرکز برش مقطع بالا در نقطه ای بر روی محور تقارن (محور z) قرار دارد. به منظور تعیین محل دقیق این نقطه، فرض می کنیم که تیر مورد نظر توسط یک نیروی برشی موازی با محور y (نیروی Vy) و حول محور z (محور خنثی) تحت خمش قرار گرفته است.

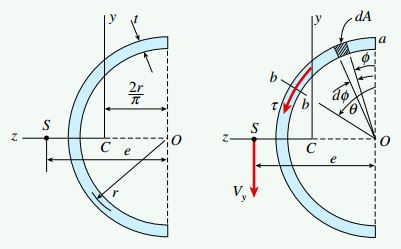
تنش های برشی:
اولین قدم تحلیل، تعیین تنش های برشی اعمال شده بر سطح مقطع است. به این منظور، مقطع bb در فاصله s از نقطه a را در نظر بگیرید.

حرف θ بر روی شکل بالا، زاویه مرکزی بین نقطه a و مقطع bb را نمایش می دهد. بنابراین، فاصله s برابر rθ (حاصل ضرب شعاع r در زاویه بین a و bb) است.

برای تعیین گشتاور اول سطح بین نقطه a و مقطع bb، المان dA را بر روی سطح مقطع مشخص کرده و سپس انتگرال زیر را محاسبه می کنیم:

φ: زاویه بین نقطه a تا المان مورد بررسی؛ t: ضخامت مقطع

به این ترتیب، تنش برشی τ در مقطع bb برابر است با:

با جایگذاری Iz=πr3t/2 (رابطه ممان اینرسی برای مقطع نازک نیم دایره) در رابطه بالا، خواهیم داشت:

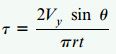
اگر θ=0 یا θ=π باشد، τ=0 خواهد بود. در θ=π/2، تنش برشی به مقدار ماکسیمم می رسد.

محل قرارگیری مرکز برش:
برآیند تنش های برشی باید به صورت یک نیروی برشی عمودی (Vy) باشد. از این رو، گشتاور حاصل از تنش های برشی (M0) حول مرکز O با گشتاور نیروی Vy حول همان نقطه یکسان خواهد بود:

برای محاسبه M0، ابتدا تنش برشی τ بر روی المان dA را با استفاده از رابطه زیر تعیین می کنیم:

به این ترتیب، گشتاور حاصل از نیروی τdA برابر است با:

از آنجایی که φdA=trd، رابطه بالا به صورت زیر بازنویسی می شود:

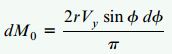
در نتیجه، گشتاور حاصل از نیروهای برشی با استفاده از رابطه زیر به دست می آیند:

اگر رابطه بالا را بر حسب e بازنویسی کنیم، خواهیم داشت:

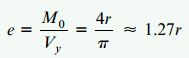
این نتیجه نشان می دهد که مرکز برش S در محلی خارج از مقطع نیمه دایره قرار گرفته است.

به عنوان یک نکته تکمیلی به خاطر داشته باشید که فاصله مرکز نیم دایره تا مرکز هندسی مقطع برابر با 2r/π یا نصف فاصله e است. بنابراین، مرکز هندسی سطح مقطع در میانه مرکز برش و مرکز نیم دایره قرار دارد.