تعیین مرکز برش در مقاطع جدار نازک باز (مقطع نبشی)

تعیین مرکز برش در مقاطع جدار نازک باز (مقطع نبشی):
شکل زیر، یک مقطع نبشی با اضلاع برابر را نمایش می دهد. طول هر یک از اضلاع این مقطع برابر با b و ضخامت آن برابر با t است.

به منظور شروع تحلیل، محور z به عنوان محور تقارن و مرکز هندسی C، به عنوان مبدأ مختصات در نظر می گیریم. به این ترتیب، هر دو محور y و z، محورهای اصلی مرکزی خواهند بود.

مرکز برش یک مقطع نبشی یا اضلاع برابر

برای تعیین موقعیت قرارگیری مرکز برش، روندی مشابه با روند ارائه شده در بخش قبلی را دنبال می کنیم. البته در ادامه خواهیم دید که محل قرارگیری مرکز برش مقطع نبشی با بررسی پیکربندی آن نیز قابل تعیین است.

به منظور شروع تحلیل، ابتدا فرض می کنیم که مقطع مورد بررسی در معرض یک نیروی برشی موازی با محور y (نیروی Vy) قرار دارد.

سپس، تنش های برشی مربوطه را با استفاده از رابطه τ=VyQz/Izt به دست می آوریم. به این منظور، گشتاور اول مساحت بین نقطه a در لبه بیرونی تیر و مقطع bb در فاصله s از نقطه a را محاسبه می کنیم.

مقدار این مساحت برابر با st و فاصله مرکز هندسی آن تا محور خنثی برابر با رابطه زیر است:

بنابراین، گشتاور سطح برابر است با:

با جایگذاری عبارت های این رابطه در رابطه τ، امکان محاسبه تنش برشی در فاصله s از لبه سطح مقطع فراهم می شود:

ممان اینرسی Iz برای نبشی مورد تحلیل (زاویه 45 درجه بین راستای محور خنثی و راستای اضلاع) از طریق رابطه زیر به دست می آید:

اگر عبارت های این رابطه را در رابطه τ قرار دهیم، به معادله زیر می رسیم:

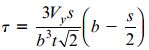
معادله، تنش برشی موجود در هر نقطه دلخواه بر روی اضلاع نبشی را به دست می آورد. رابطه بین فاصله s با تغییرات تنش حاصل در این معادله، از نوع رابطه درجه چهار است (شکل زیر).

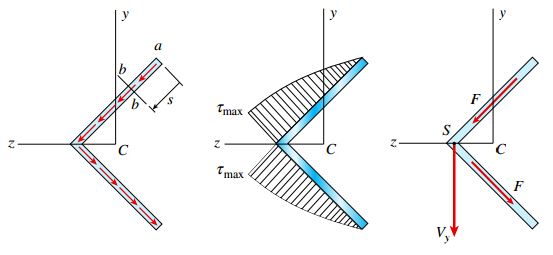
با توجه به نمودار بالا، تنش برشی ماکسیمم در محل تقاطع اضلاع نبشی رخ می دهد. بنابراین، برای تعیین مقدار این تنش باید s را برابر b قرار دهیم:

نیروی برشی F در هر یک از اضلاع نبشی با حاصل ضرب نمودار تنش در ضخامت آن ضلع برابر است:

مؤلفه های افقی نیروهای F یکدیگر را خنثی می کنند. به همین دلیل، تنها اثر مؤلفه های عمودی آن ها باقی می ماند.

هر یک از این مؤلفه های عمودی برابر 2√/F یا Vy/2 هستند.

از این رو، برآیند نیروی عمودی با نیروی برشی Vy برابری می کند. به دلیل عبور نیروی برآیند از محل تقاطع خط اثرهای دو نیروی F، مرکز برش S در محل تقاطع دو ضلع نبشی قرار خواهد داشت.