ضریب شکل و مدول پلاستیک

ضریب شکل و مدول پلاستیک:

رابطه به دست آمده برای گشتاور پلاستیک را می توان بر حسب رابطه گشتاور تسلیم نیز بازنویسی کرد:

که در آن:

Z، مدول پلاستیک سطح مقطع است. از نظر هندسی، این مدول را می توان به عنوان گشتاور اول سطح بالای محور خنثی به علاوه گشتاور اول سطح زیر محور خنثی در نظر گرفت.

نسبت گشتاور پلاستیک به گشتاور تسلیم فقط تابعی از شکل سطح مقطع بوده و با عنوان «ضریب شکل» (Shape Factor) شناخته می شود:

این ضریب، معیاری از مقاومت ذخیره شده در تیر بعد از شروع اولین تسلیم است.

مقدار ضریب شکل برای مواردی که بخش زیادی از سطح مقطع در نزدیکی محور خنثی قرار داشته باشد (مانند تیری با سطح مقطع دایره ای توپر) دارای بیشترین مقدار و برای مواردی که بخش زیادی از سطح مقطع در فاصله دور از محور خنثی قرار داشته باشد (مانند تیری با سطح مقطع بال پهن) دارای کمترین مقدار است.

نحوه تعیین مقادیر f برای سطح مقطع های مستطیلی، بال پهن و دایره ای در بخش های بعدی تشریح خواهد شد.

سطح مقطع تیر مستطیلی:
شکل زیر، یک تیر با سطح مقطع مستطیلی را نمایش می دهد. جنس این تیر از مواد الاستوپلاستیک و مدول مقطع آن S=bh2/6 است.

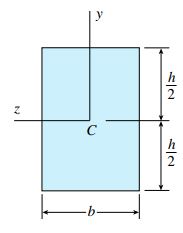
سطح مقطع مستطیلی

بنابراین، گشتاور تسلیم تیر بالا از رابطه زیر به دست می آید:

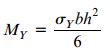
b: عرض سطح مقطع؛ h: ارتفاع سطح مقطع

به دلیل وجود تقارن مضاعف در سطح مقطع مستطیلی، محور خنثی آن در تمام محدوده های بارگذاری (الاستیک یا پلاستیک) از مرکز هندسی عبور می کند. از این رو، فاصله مراکز هندسی نواحی بالا و پایین تا محور خنثی برابرند با:

به این ترتیب، مدول پلاستیک برابر است با:

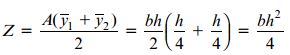
و برای گشتاور پلاستیک داریم:

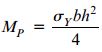
در نهایت، ضریب شکل مقطع مستطیلی از رابطه زیر به دست می آید:

یعنی گشتاور پلاستیک یک تیر مستطیلی 50 درصد بزرگ تر از گشتاور تسلیم است. اکنون تنش های موجود در یک تیر مستطیلی را برای حالتی در نظر بگیرید که گشتاور خمشی M بزرگ تر از گشتاور تسلیم بوده اما به گشتاور پلاستیک نرسیده باشد.

در این شرایط، بخش های خارجی تیر تحت تنش تسلیم σY و بخش های داخلی (هسته الاستیک) در معرض تنش با تغییرات خطی هستند (شکل زیر).

نواحی پلاستیک کامل با رنگ خاکستری و فاصله محور خنثی تا لبه داخلی این نواحی با حرف e نمایش داده شده است.

تنش های اعمال شده بر سطح مقطع دارای نیروی برآیند T1، C2، C1 و T2 هستند. هر یک از نیروهای C1 و T1 در نواحی پلاستیک با حاصل ضرب تنش تسلیم در مساحت این نواحی برابری می کند:

نیروهای C2 و T2 در ناحیه هسته الاستیک نیز برابر با حاصل ضرب مساحت این ناحیه بر روی نمودار تنش در عرض b هستند:

به این ترتیب، برای گشتاور خمشی داریم:

توجه داشته باشید که اگر e=h/2 باشد، M=MY و در صورتی که e=0 باشد، M=3My/2 یا همان گشتاور پلاستیک MP خواهد بود.

در صورت مشخص بودن ابعاد هسته الاستیک می توان رابطه بالا را برای تعیین گشتاور خمشی به کار برد.

با این وجود، معمولاً از گشتاور خمشی به منظور محاسبه اندازه هسته الاستیک استفاده می شود.

بنابراین، اگر این رابطه را بر حسب گشتاور خمشی بازنویسی کنیم؛ خواهیم داشت:

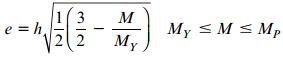
در اینجا نیز توجه داشته باشید که بر اساس شرایط مرزی اگر M=MY باشد، e=h/2 و در صورتی که M=MP=3MY/2 یا در حالت پلاستیک کامل باشد، e=0 خواهد بود.

سطح مقطع تیر بال پهن:
شکل زیر، یک تیر بال پهن با تقارن مضاعف را نمایش می دهد. مدول پلاستیک Z این تیر از گشتاور اول سطح یکی از بال ها به علاوه گشتاور اول بخش بالایی جان و ضرب مقدار به دست آمده در 2 تعیین می شود.

شکل ساده تر رابطه بالا را می توان به صورت بازنویسی کرد:

به این ترتیب، مدول پلاستیک از رابطه بالا و گشتاور پلاستیک با قرار دادن Z در رابطه MP=σYZ به دست می آید. مقادیر Z برای انواع مختلف تیرهای بال پهن را می توان در منابع مختلف یافت.

ضریب شکل f برای تیرهای بال پهن معمولاً از مقدار 1.1 تا 1.2 تغییر می کند. این مقدار به نسبت بین بخش های سطح مقطع تیر بستگی دارد.

به منظور تحلیل تیرهای دارای اشکال دیگر نیز می توان از فرآیندی مشابه با فرآیند تشریح شده در این بخش استفاده کرد.