حل مسائل دینامیکی چگونه انجام می شود؟
محاسبات دینامیکی با در نظر گرفتن ضربه ناشی از نیروی اینرسی در تمام بازه های زمانی صورت می گیرند.
وجود نیروی اینرسی، حل مسئله را دشوارتر می کند اما با درک صحیح و استفاده از روش های مناسب می توان پیچیدگی های موجود را ساده تر کرد. یکی از متداول ترین روش های ساده سازی و حل مسائل دینامیک سازه، روش گسسته سازی است.
گسسته سازی چیست و چه کاربردی در دینامیک سازه دارد؟
نیروی اینرسی، اصلی ترین دلیل عکس العمل سازه در برابر بارهای دینامیکی است. منشا این نیرو، به جرم سازه بازمی گردد.
به همین دلیل، تعریف موقعیت مکانیکی و حرکت سازه با توجه به جرم آن، یکی از عوامل کلیدی در فرآیند تحلیل دینامیک خواهد بود. علاوه بر این، جرم سازه، محل قرارگیری و نحوه حرکت آن بر روی تعیین درجه آزادی دینامیکی و استاتیکی نیز تأثیرگذار است.
در نتیجه، انتخاب صحیح درجه آزادی دینامیکی، اهمیت زیادی در تعریف دقیق نیروی اینرسی دارد.
تمام سیستم های سازه ای دارای جرم گسترده و بی نهایت درجه آزادی هستند. تحلیل دینامیک سازه ای با بی نهایت درجه آزادی کار بسیار دشواری است. به منظور جلوگیری از پیچیدگی محاسبات ریاضی در این نوع تحلیل، سازه مورد بررسی به سیستمی با درجه آزادی محدود تبدیل می شود.
به این کار، فرآیند گسسته سازی سازه می گویند. از رایج ترین روش های گسسته سازی می توان به روش «جرم نقطه ای» (Lumped Mass)، «جابه جایی تعمیم یافته» (Generalized Displacement) و «المان محدود» (Finite Element) اشاره کرد.
گسسته سازی به عنوان روش اصلی تبدیل مسائلی با درجه آزادی نامحدود به مسائلی با درجه آزادی محدود محسوب می شود. در ادامه به معرفی روش های متداول گسسته سازی می پردازیم.
کاربرد روش جرم نقطه ای در تحلیل دینامیک سازه چیست؟
روش جرم نقطه ای یا جرم متمرکز، متداول ترین روش مورد استفاده در ساده سازی فرآیند تحلیل دینامیک سازه است.
در این روش با استفاده از یک سری قوانین خاص، نقاطی از سازه به عنوان معرف رفتار آن انتخاب شده و سیستمی با درجه آزادی نامحدود به سیستمی با درجه آزادی محدود تبدیل می شود. تصویر زیر، مثالی از این تبدیل را با استفاده از روش جرم نقطه ای برای سازه ای با جرم گسترده نمایش می دهد.
در این تصویر، جرم گسترده m توسط سه جرم نقطه ای m2، m1 و m3 جایگزین شده است. با در نظر گرفتن جابه جایی جانبی در سطح مقطع، تیر با جرم های نقطه ای دارای سه درجه آزادی جانبی خواهد بود.
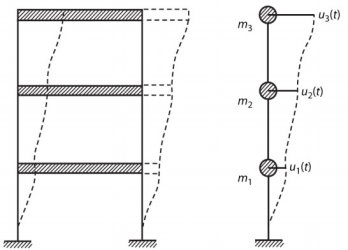
تصویر زیر، مثال دیگری از تبدیل درجه آزادی نامحدود به درجه آزادی محدود را برای یک ساختمان سه طبقه نمایش می دهد. در این مثال، اگر جرم نیمی از ستون ها، دیوارها، کف و تیرهای هر طبقه را در مرکز کف طبقه متمرکز کنیم، تعداد درجات آزادی این ساختمان از بی نهایت به سه درجه آزادی کاهش می یابد.
کاربرد روش مختصات یا جابه جایی تعمیم یافته در تحلیل دینامیک سازه چیست؟
مختصات تعمیم یافته، پارامترهای مستقلی هستند که به منظور نمایش محل قرارگیری سیستم مورد استفاده قرار می گیرند.
به کارگیری مختصات تعمیم یافته در سیستم تیر با جرم گسترده می تواند دقت محاسبات را افزایش دهد. به منظور حل معادلات دیفرانسیل معمولا از دنباله یا سری استفاده می شود. در دینامیک سازه می توان تغییر شکل سازه هایی نظیر تیر را با سری فوریه بیان کرد.
به عنوان مثال، سری فوریه برای تیر نمایش داده شده در تصویر بالا به صورت زیر است:
در این رابطه:
به دلیل مشخص بودن تابع شکل، تغییر شکل تیر توسط چندین مختصات تعمیم یافته تعیین می شود. در تحلیل دینامیک تئوری، تعداد درجات آزادی تیر ساده نامحدود خواهد بود. با این وجود، در تحلیل واقعی، فقط چند جمله اول سری فوریه مورد استفاده قرار می گیرند.
به این ترتیب، سیستم تیر به یک سیستم با N درجه آزادی تبدیل می شود. عبارت تعمیم یافته برای بیان جابه جایی سازه را می توان به صورت زیر نوشت:
در مثال تیر ساده، شرطی که تابع شکل باید در آن صدق کند عبارت است از:
φn(O)=φn(L)=0
اگر تابع شکل، جابه جایی سازه را نشان دهد، مختصات تعمیم یافته با جابه جایی هم بعد خواهد شد.
مختصات تعمیم یافته می تواند نمایش دهنده دامنه تابع شکل باشد اما جابه جایی نمایش داده شده در این تابع واقعی نخواهد بود؛ زیرا جابه جایی واقعی زمانی به دست می آید که تمام N جمله سری در محاسبات در نظر گرفته شده باشند.
کاربرد روش المان محدود در تحلیل دینامیک سازه چیست؟
«روش المان محدود» (Finite Element Method) یا به اختصار FEM، ترکیبی از روش های جرم نقطه ای و مختصات تعیم یافته است که برای حل مسائل استاتیک و دینامیک سازه مورد استفاده قرار می گیرد.
در فرآیند FEM، سازه به صورت مجموعه ای از نقاط (نقاط گره ای) تعریف می شود. جابه جایی هر یک از نقاط گره ای، بیانگر وضعیت جابه جایی نقطه متناظر آن در سازه واقعی است.
در فرآیند گسسته سازی FEM، با اضافه کردن جابه جایی های فرضی به المان ها، منحنی تغییر شکل کل سازه در یک زمان مشخص به دست می آید.
سپس منحنی های معرف شکل المان ها، به صورت تابع جابه جایی یا درون یابی با چندین پارامتر مختلف تعریف می شوند. توابع جابه جایی باید درون هر المان به صورت پیوسته و مطابق محدودیت های موجود در دو انتهای المان باشند.
با توجه به این موارد، پارامترهای دخیل در تابع جابه جایی را می توان توسط جابه جایی گره ای تعریف کرد. به این ترتیب، سیستمی با درجه آزادی نامحدود به سیستمی با درجه آزادی محدود و جابه جایی گره ای نامشخص تبدیل می شود.
به عنوان مثال، یک تیر پیوسته را در نظر بگیرید. این تیر را می توان به N المان (قطعات تیر) تقسیم کرد. محل تقاطع المان های مجاور با عنوان نقاط گره ای شناخته می شود.
پارامترهای جابه جایی گره ای (جابه جایی u و زاویه دوران θ) به عنوان مختصات تعمیم یافته سیستم مورد استفاده قرار می گیرند.
این مدل المان محدود دارای شش مختصات تعمیم یافته با پارمترهای جابه جایی زیر است:
u1,θ1,u2,θ2,u3,θ3
توابع شکل نیز به صورت زیر هستند:
φ1,φ2,φ3,φ4,φ5,φ6
برای مدل گسسته تیر یکسرگیردار با N المان، در مجموع 2N مختصات تعمیم یافته وجود دارد. به علاوه، جابه جایی تیر نیز توسط 2N مختصات تعمیم یافته و توابع شکل آن ها به صورت زیر قابل تعریف است:
u(x)=u1φ1(x)+θ1φ2(x)+⋯+uNφ2N−1(x)+θNφ2N(x)
به این ترتیب، یک تیر با درجه آزادی نامحدود به سیستمی با درجه آزادی 2N تبدیل می شود. فرآیند روش المان محدود، ویژگی های روش جرم نقطه ای و مختصات تعمیم یافته را به صورت زیر ترکیب می کند:
مقایسه روش های گسسته سازی در دینامیک سازه:
از میان روش های مرکز جرم، مختصات تعمیم یافته و المان محدود، روش اول، ساده تر و کاربردی تر است. روش مختصات تعمیم یافته به انتخاب تابع شکل مناسب برای صدق کردن در شرایط مرزی جابه جایی نیاز دارد. این مسئله، کاربرد روش مذکور را به سازه های ساده محدود می کند.
به دلیل ترکیب ویژگی های دو روش اول در FEM، این روش به منظور تحلیل سازه های پیچیده و حل مسائل دینامیک سازه به طور گسترده مورد استفاده قرار می گیرد.
|
|
|
|
| نماد اعتماد الکترونیک | نشان ملی ثبت | گواهی شامد ارشاد |
© کلیه حقوق مادی و معنوی این وب سایت متعلق به داده پردازان هومان پویان می باشد.
